Convolution

In this section we will have a look at the math behind convolutional layers and the hyperparameters that can be used to modify their behaviour.

What is convolution?

In the context of convolutional models, convolution refers to a mathematical operation that is performed on two functions to produce a third function. In the case of convolutional neural networks (CNNs), this operation is used to process input data, such as images, in order to extract meaningful features.

At its core, convolution involves sliding a small window, called a kernel or filter, across the input data. The kernel is usually a small matrix of weights. Each position of the kernel corresponds to a specific element in the input data, and the weights in the kernel determine the contribution of that element to the output.

As the kernel slides across the input, it performs a dot product between its weights and the values in the region of the input it is currently positioned on. This dot product is then summed up to produce a single value, which becomes the corresponding element in the output feature map. The process is repeated for each position of the kernel until the entire input has been covered.

The key idea behind convolutional neural networks is that the kernels used in the convolution operation are learned through training. This means that the network learns to automatically determine the best weights for each kernel, enabling it to extract relevant features from the input data.

Convolutional layers are typically stacked in CNNs, allowing the network to learn increasingly complex features as information flows through the layers. The outputs of one convolutional layer are often passed through non-linear activation functions, such as ReLU, to introduce non-linearity into the model.

Convolutional models have been highly successful in various computer vision tasks, such as image classification, object detection, and image segmentation, due to their ability to capture local patterns and spatial relationships in the input data.

A simple example

Let's illustrate how convolution is performed on a 5x1 2D array using a 3x1 kernel. Here's an example:

Step 1

The kernel is slided from left to right along the input sequence. In each step of the convolution process the cells of the kernel are multiplied with those cells of the input sequence they overlap. In this example the number 2 of the input sequence would be overlapped by the number 2 of the kernel, 5 of the input sequence would be overlapped by 1 of the kernel and 3 of the input sequence would be overlapped by 3 of the kernel.

All overlapping numbers are multiplied and finally the results of the multiplication are added. In this example we get the following result for the first convolution step: 2*2 + 5*1 + 3*3 = 18. The resulting number is than saved in the output sequence.

Step 2

In the next step the kernel is slided one position to the right. Again the overlapping numbers are multiplied and then added. This time we get the following result: 5*2 + 3*1 + 1*3 = 16.

Step 3

This process is repeated until the kernel reaches the end of the sequence. In our example this is the case when we again shift the kernel one position to the right. This time we get the result 3*2 + 1*1 -4*3 = -5.

You can see that the ouput sequence is shorter than the input sequence. The larger the kernel is the smaller gets the output sequence.

Using convolution for finding patterns

Convolution can be used to find patterns. Have a look at the following sequence of numbers. The pattern (2,5,3) appears multiple times in the input sequence. As the kernel is slided over this pattern it always produces the same output in the target sequence, which is 18 in this example.

We can use this in audio signals or images to find patterns like edges or more complex features within the data. The more kernels we use the more features can be found in the input sequence.

Stride

In the context of neural networks, stride refers to the step size or the amount of movement applied to the sliding window (kernel) during the convolution operation. It determines how much the window is shifted after each convolution operation.

When performing convolution, the stride value determines how much the window moves horizontally and vertically across the input data. A stride of 1 means that the window moves one step at a time, resulting in overlapping receptive fields. A larger stride value, such as 2, means that the window skips positions and moves two steps at a time, resulting in non-overlapping receptive fields.

The main implications of stride in neural networks are:

Output spatial dimensions: The stride value affects the spatial dimensions of the output feature map. As the stride increases, the output size decreases because the window covers fewer positions of the input data. The relationship between the input size (height and width), kernel size, stride, and output size is given by the following formula:

output_height = (input_height - kernel_height) / stride + 1
output_width = (input_width - kernel_width) / stride + 1

Information preservation: Larger stride values result in a loss of information compared to smaller stride values. With a larger stride, the window skips positions, and the receptive fields of the output feature map do not overlap as much with the input data. This can lead to a coarser representation of the input and potentially loss of fine-grained details.

Computational efficiency: Using a larger stride can reduce the computational cost of the convolution operation. With a larger stride, fewer positions need to be processed, reducing the number of multiplications and additions required. This can be beneficial in terms of memory usage and computational efficiency, especially in models with large input sizes or complex architectures.

It's worth noting that adjusting the stride is closely related to the concept of padding. When the stride is greater than 1, the output size decreases, and it may not cover the entire input size. In such cases, padding can be used to retain the spatial dimensions of the input and ensure that the output feature map covers the entire input.

Stride is a hyperparameter that can be tuned during the design of a neural network architecture. The choice of stride value depends on various factors, including the nature of the problem, the size of the input data, and the desired output resolution.

Padding

Padding is a technique used in convolutional neural networks (CNNs) to adjust the size of the input data and the output feature maps during the convolution operation. It involves adding extra rows and columns of zeros around the input data before performing the convolution.

The main reasons for using padding are:

Preserve spatial dimensions: Convolution reduces the spatial dimensions of the input data. By adding padding, we can retain the spatial dimensions of the input and output feature maps. This can be important in cases where the spatial information is critical, such as in image segmentation or object localization tasks.

Mitigate border effects: When convolving a kernel over the edges of the input data, the resulting output feature map may be smaller than the input. This can lead to the loss of information at the borders. Padding helps mitigate this issue by providing additional context around the edges, allowing the convolutional operation to be performed more accurately.

Pooling

Pooling is a down-sampling operation commonly used in convolutional neural networks (CNNs) to reduce the spatial dimensions of the feature maps generated by the convolutional layers. It helps in simplifying and abstracting the learned representations while retaining the most important information.

There are different types of pooling operations, but the two most common ones are max pooling and average pooling:

Max Pooling: Max pooling divides the input feature map into non-overlapping rectangular regions (pools) and outputs the maximum value within each pool. By taking the maximum value, max pooling retains the most activated or dominant features within each pool. It helps in capturing the presence of certain features regardless of their exact location, making the network more robust to translations and local variations. Max pooling reduces the spatial dimensions of the feature maps while preserving the most salient information.

Average Pooling: Average pooling is similar to max pooling, but instead of taking the maximum value within each pool, it calculates the average value. Average pooling is useful when the magnitude or intensity of the features is important rather than their specific locations. It can help in reducing the noise or variations in the feature maps and can be used as an alternative to max pooling in some cases.

Pooling brings several benefits to CNNs:

Dimensionality reduction: Pooling reduces the spatial dimensions of the feature maps, which can help in reducing the computational complexity of the network. By reducing the number of parameters and computations, pooling enables more efficient training and inference.

Translation invariance: Max pooling, in particular, helps in capturing the presence of important features regardless of their exact location. This translation invariance property makes CNNs more robust to variations in object position, rotation, or scale within an image.

Feature abstraction: Pooling helps in abstracting the representations learned by the convolutional layers. By summarizing the most important or activated features within each pool, pooling operations capture higher-level patterns and reduce the sensitivity to local variations or noise.

It's worth noting that pooling is typically applied after the convolutional layers in a CNN, and it is often used in conjunction with convolution to down-sample and abstract the feature maps. The choice of pooling operation and its parameters (such as pool size and stride) depends on the specific problem and network architecture.

Using multiple Kernels

When performing convolution with multiple kernels, also known as multi-channel convolution, each kernel corresponds to a separate feature map in the output. The process involves convolving each kernel with the input data independently and producing a separate feature map for each kernel.

Using multiple convolution layers

TODO

2D convolutions

Convolution can also be performed with 2D matrices. In fact, convolution with 2D matrices is a fundamental operation in image processing and computer vision tasks.

When performing convolution with 2D matrices, the process is very similar to the convolution with 1D arrays or 2D arrays. Instead of using a 1D kernel or a 2D kernel, a 2D convolution involves using a 2D filter or kernel to slide over the input matrix and perform element-wise multiplication followed by summation.

Here's an example to illustrate 2D convolution with matrices:

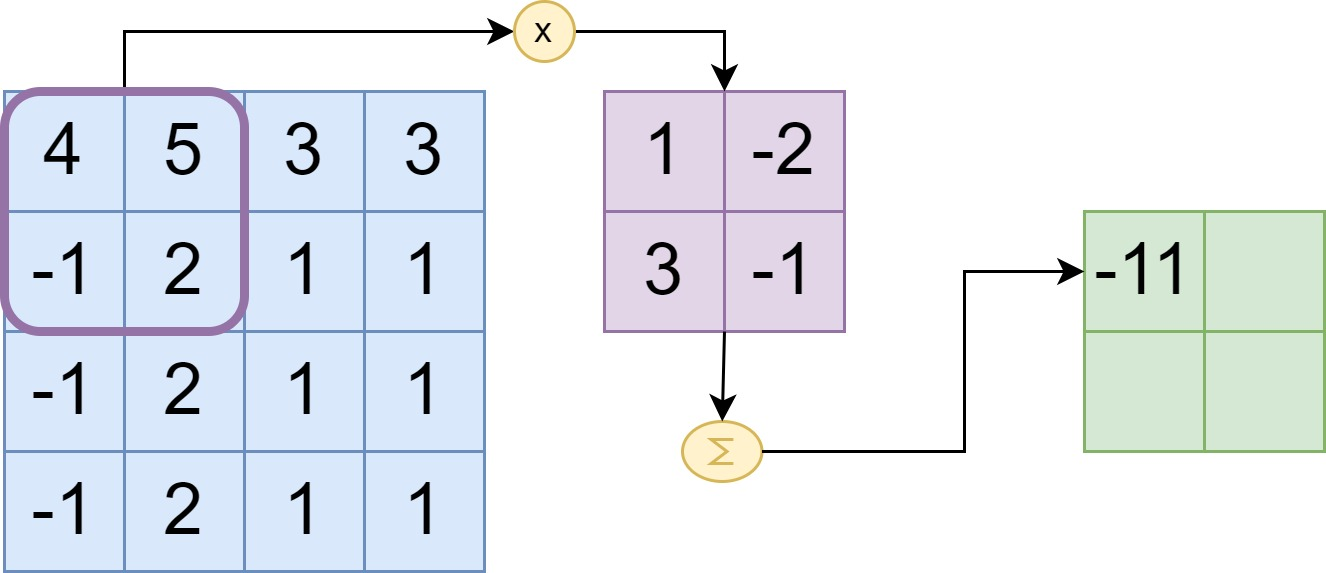
In this example we have a 2x2 kernel that is slided with a stride of two over a 2D input matrix (which could be a grayscale image). The output is computed by first multiplying the kernel cells with the corresponding cells in the overlapped part of the input matrix. Next the resuls of the multiplications are added. The first cell is of the output matrix is computed as follows: 4*1 + 5*-2 -1*3 + 2*-1 = -11

3D Tensor convolutions

The same can be done with 3D tensors or even higher-dimensional tensors. In this example we slide a 3x3x3 kernel over a 5x5x3 input matrix. This will result in a 3x3x1 output matrix. When we use convolutional layers for processing RGB-colored images we usually transform these input images into 3D tensors. The first two dimensions correspond to the width and height of the image, the third dimension corresponds to the color channels (red + green + blue)